2172-, [2072-][1972-][1872-][1772-][1672-][1572-][1472-][1372-][1272-][1172-][1072-][972-][872-][772-][672-][572-][472-][372-][272-][172-][72-] / sort : [↓-]. ↑
 |  |  |  |  |
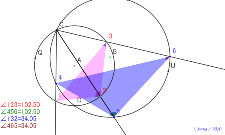
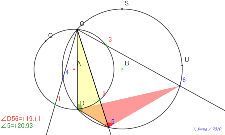
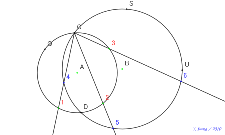
| 02185-Enn | 02184-円の距離 | 02183- 相似になる基本の２円 番号で三角形を２つの円の交点をたくさん とる | 02182- ダメ3基本の２円 番号で三角形を２つの円の交点をたくさんとる | 02181- ダメ2１基本の２円 番号で三角形を２つの円の交点をたくさんと る |
 |  |  |  |  |
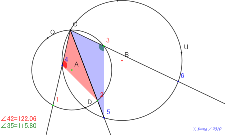
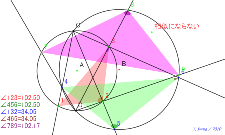
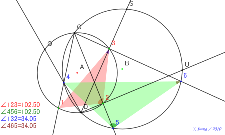
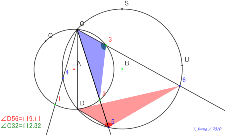
| 02180- ダメ１基本の２円 番号で三角形を２つの円の交点をたくさんとる | 02179- 基本の２円 番号で三角形を２つの円の交点をたくさんとる | 02178- これは相似にならない相似になる番号で三角形を２つの円の交点を たくさんとる | 02177- 相似になる番号で三角形を２つの円の交点をたくさんとる | 02176- 番号で三角形を２つの円の交点をたくさんとる |
 |  |  |  |  |
| 02175- 相似になる。２つの円と相似な三角形 | 02174- 相似にならないダメ！！相似かな？角度たくさん測定相似にならな いダメその２ ２つの円の交点をたくさんとる | 02173- 相似かな？角度たくさん測定相似にならないダメその２ ２つの円 の交点をたくさんとる | 02172- 角度たくさん測定相似にならないダメその２ ２つの円の交点をた くさんとる | 02171- 角度たくさん測定相似にならないダメその２ ２つの円の交点をた くさんとる |
 |  |  |  |  |
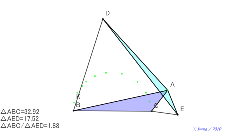
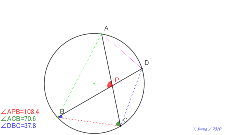
| 02170- 相似にならないダメその２ ２つの円の交点をたくさんとる | 02169- 相似にならないダメ２つの円の交点をたくさんとる | 02168- ２つの円の交点をたくさんとる | 02167- sinも直角三角形にすれば、△AEDはその半分の面積になる。 理由は？ | 02166- sinも直角三角形にすれば、△AEDはその半分の面積になる。 理由は？ |
 |  |  |  |  |
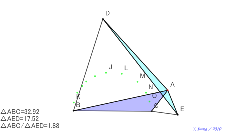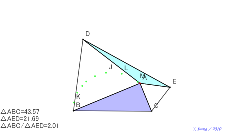
| 02165- sinも直角三角形にすれば、△AEDはその半分の面積になる。 理由は？ | 02164- sinmo直角三角形にすれば、△AEDはその半分の面積になる 。理由は？ | 02163- 記録を取る赤円周上に点Aを置けば、面積は２倍（正三角形を乗せ るとき） | 02162- 記録を取る赤円周上に点Aを置けば、面積は２倍（正三角形を乗せ るとき） | 02161- 記録を取る赤円周上に点Aを置けば、面積は２倍（正三角形を乗せ るとき） |
 |  |  |  |  |
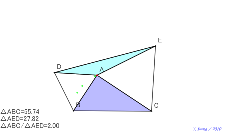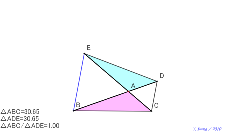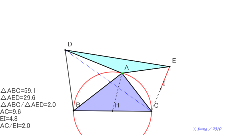
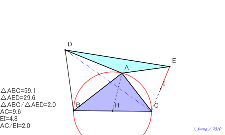
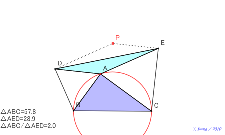
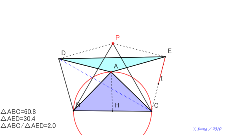
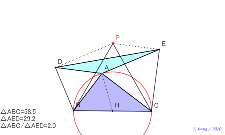
| 02160- 記録を取る赤円周上に点Aを置けば、面積は２倍（正三角形を乗せ るとき） | 02159- 面積が一致する青と紫線が一致すれば、２つの三角形の面積が同じ になる。点Aの軌跡は？ | 02158- 証明が出来た △DCEは二等辺三角形、点Iは辺ACの半分の長 さ 考え中？動かない点は、正三角形BCPで頂点平行四辺形を作 って2倍にして考える。直角三角形にすれば、△AEDはその半分 の面積になる。理由は？ | 02157- 証明が出来た △DCEは二等辺三角形、点Iは辺ACの半分の長 さ 考え中？動かない点は、正三角形BCPで頂点平行四辺形を作 って2倍にして考える。直角三角形にすれば、△AEDはその半分 の面積になる。理由は？ | 02156- △DCEは二等辺三角形、点Iは辺ACの半分の長さ 考え中？動 かない点は、正三角形BCPで頂点平行四辺形を作って2倍にして 考える。直角三角形にすれば、△AEDはその半分の面積になる。 理由は？ |
 |  |  |  |  |
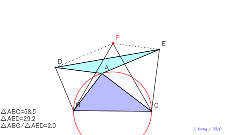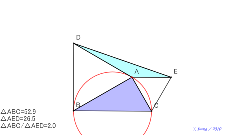
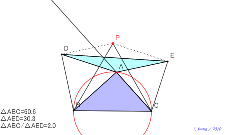
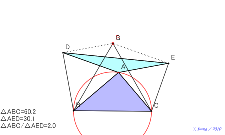
| 02155- 考え中？動かない点は、正三角形BCPで頂点平行四辺形を作って 2倍にして考える。直角三角形にすれば、△AEDはその半分の面 積になる。理由は？ | 02154- 考え中？動かない点は、正三角形BCPで頂点平行四辺形を作って 2倍にして考える。直角三角形にすれば、△AEDはその半分の面 積になる。理由は？ | 02153- 考え中？動かない点は、正三角形BCPで頂点平行四辺形を作って 2倍にして考える。直角三角形にすれば、△AEDはその半分の面 積になる。理由は？ | 02152- 動かない点は、正三角形BCPで頂点平行四辺形を作って2倍にし て考える。直角三角形にすれば、△AEDはその半分の面積になる 。理由は？ | 02151- 平行四辺形を作って2倍にして考える。直角三角形にすれば、△A EDはその半分の面積になる。理由は？ |
 |  |  |  |  |
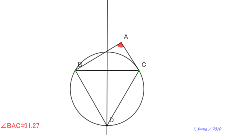
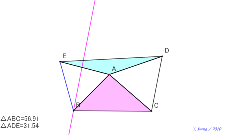
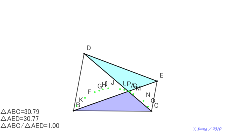
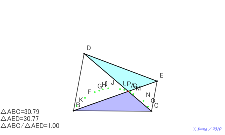
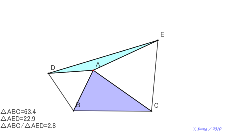
| 02150- 直角三角形にすれば、△AEDはその半分の面積になる。理由は？ | 02149-円周角１２０°の作り方 | 02148-円周角１２０°の作り方 | 02147-円周角１２０°の作り方 | 02146- ∠DAE＝９０°、∠BAC＝１５０°になると、逆半分になる |
 |  |  |  |  |
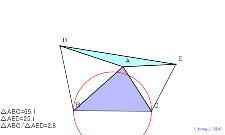| 02145- 赤円周上に点Aを置けば、面積は２倍（正三角形を乗せるとき） | 02144- 青と紫線が一致すれば、２つの三角形の面積が同じになる。点Aの 軌跡は？ | 02143- この曲線はなにか？２つの三角形の面積は、同じ普通の三角形の辺 に正三角形を乗せる | 02142- この曲線はなにか？２つの三角形の面積は、同じ普通の三角形の辺 に正三角形を乗せる | 02141- ２つの三角形の面積は、同じ普通の三角形の辺に正三角形を乗せる |
 |  |  |  |  |
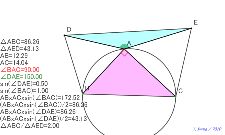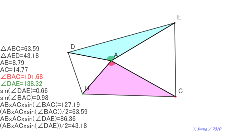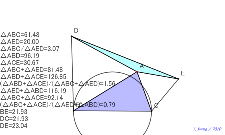| 02140- ２つの三角形の面積は、同じ普通の三角形の辺に正方形を乗せる | 02139- 点Fが不動点？？２つの面積は、どこで半分なるか？sin使った | 02138- ２つの面積は、どこで半分なるか？sin使った | 02137- ２つの面積は、どこで等しくなるか？sin使った | 02136- 普通の三角形と２つの正三角形 |
 |  |  |  |  |
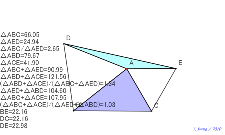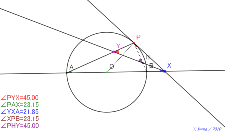
| 02135- 普通の三角形と２つの正三角形 | 02134- 正三角形の色を消す証明に使う？？二等辺三角形ができる 普通の 三角形の上に正三角形 ７個の中点 | 02133- 証明に使う？？二等辺三角形ができる 普通の三角形の上に正三角 形 ７個の中点 | 02132- 証明に使う？？二等辺三角形ができる 普通の三角形の上に正三角 形 ７個の中点 | 02131- 時間切れ 等しい角度のペアあり 角の三等分線でどうなるか？ 円Oと直径の延長線と接線PX |
 |  |  |  |  |
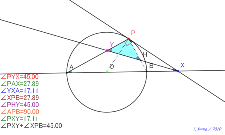| 02130- 半径を点線で 角の二等分線で４５° 円Oと直径の延長線と接線 PX | 02129- 相似な三角形が一組 等しい角度のペアあり 角の三等分線でどう なるか？ 円Oと直径の延長線と接線PX | 02128- 等しい角度のペアあり 角の三等分線でどうなるか？ 円Oと直径 の延長線と接線PX | 02127- 二等編三角形に色付ける 接弦定理で証明 内角と外角の和で 角 の二等分線で４5° 円Oと直径の延長線と接線PX | 02126- 接弦定理で証明 内角と外角の和で 角の二等分線で４5° 円O と直径の延長線と接線PX |
 |  |  |  |  |
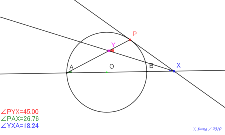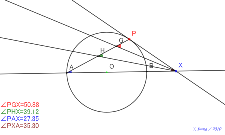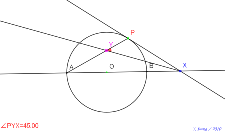
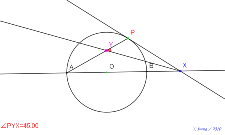
| 02125- 内角と外角の和で 角の二等分線で４5° 円Oと直径の延長線と 接線PX | 02124- 角の三等分線でどうなるか？ 円Oと直径の延長線と接線PX | 02123- 角の三等分線で３倍 円Oと直径の延長線と接線PX | 02122- 角の二等分線で４5° 円Oと直径の延長線と接線PX | 02121- 角の二等分線で４5０° 円Oと直径の延長線と接線PX |
 |  |  |  |  |
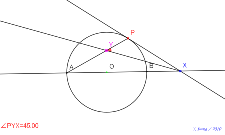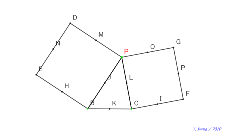
| 02120- 角の二等分線で４０° 円Oと直径の延長線と接線PX | 02119- 円Oと直径の延長線と接線PX | 02118-円Oと直径の延長線 | 02117-円O | 02116- 三角形と正方形とたくさんの中点を結ぶ三角形は？ |
 |  |  |  |  |
| 02115- 頂点Pだけ動点 普通の三角形の上に正三角形 ７個の中点 | 02114- 色補助線4本 アルハゼンの定理 色つき補助線あり | 02113- 色補助線３本 アルハゼンの定理 色つき補助線あり | 02112- 三角形に色付け 補助線１本 アルハゼンの定理 | 02111- 補助線１本 アルハゼンの定理 |
 |  |  |  |  |
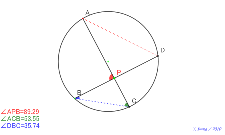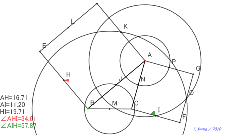| 02110- ABは固定・Pは自由アルハゼンの定理 | 02109- ABは固定・Pは自由アルハゼンの定理 | 02108- 和と差を計算する アルハゼンの定理 | 02107- 色補助線２本 アルハゼンの定理 色つき補助線あり | 02106- 特別な三角形は無さそうダメだ中点をたくさんとる三角形と正方形 と中点を結ぶ三角形は？ |
 |  |  |  |  |
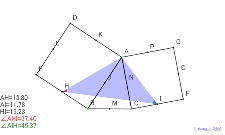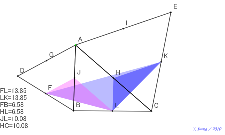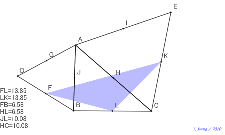
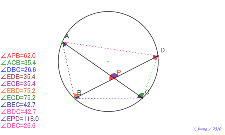
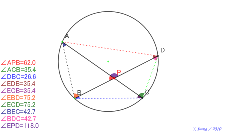
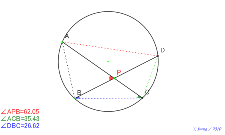
| 02105- 中点をたくさんとる三角形と正方形と中点を結ぶ三角形は？ | 02104- 種名出来た 証明は？？二等辺三角形ができる 普通の三角形の上 に正三角形 ７個の中点 | 02103- 証明は？？二等辺三角形ができる 普通の三角形の上に正三角形 ７個の中点 | 02102- たくさんの角度を測定するアルハゼンの定理 色つき補助線あり | 02101- たくさんの角度を測定するアルハゼンの定理 色つき補助線あり |
 |  |  |  |  |
| 02100- アルハゼンの定理 色つき補助線あり | 02099- 三角形と底辺の中点正三角形ならば正三角形になる | 02098- 三角形と底辺の中点正方形ではダメ | 02097-三角形と底辺の中点 | 02096-線分 |
 |  |  |  |  |
| 02095-アルハゼンの定理 1 | 02094-アルハゼンの定理 1 | 02093-アルハゼンの定理 ２ | 02092-アルハゼンの定理 ２ | 02091- アルハゼンの定理 補助線あり |
 |  |  |  |  |
| 02090-アルハゼンの定理 その２ | 02089-アルハゼンの定理 その２ | 02088- アルハゼンの定理 角度あり 補助線あり | 02087-アルハゼンの定理 角度なし | 02086-アルハゼンの定理 角度なし |