[2172-][2072-][1972-][1872-][1772-][1672-][1572-][1472-][1372-][1272-][1172-][1072-][972-][872-]772-, [672-][572-][472-][372-][272-][172-][72-] / sort : [↓-]. ↑
 |  |  |  |  |
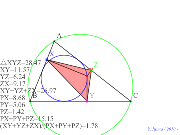
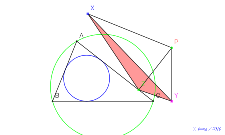
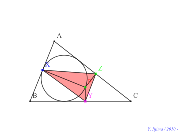
| 00772- シムダン線を内接円に。垂心三角形の重心の軌跡 | 00771- シムダン線を内接円に。垂心三角形の内心の軌跡 | 00770- シムダン線を内接円に。垂心三角形の外心の軌跡 | 00769- シムダン線を内接円に。基本の図 | 00768- シムダン線？線分の和や比駄目 |
 |  |  |  |  |
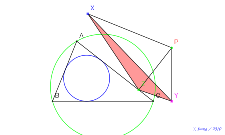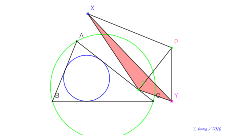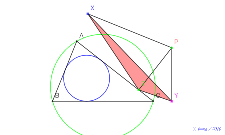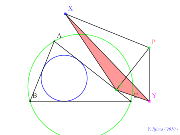| 00767-シムダン線？ | 00766-ダダン線？ | 00765-シムダン線？ | 00764- シムダン線の前後で何が起こるか？ | 00763-9 |
 |  |  |  |  |
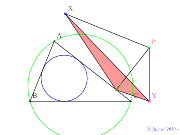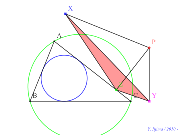
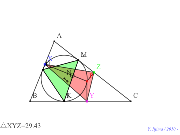
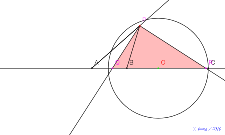
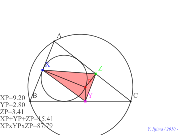
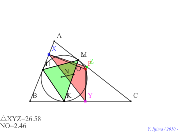
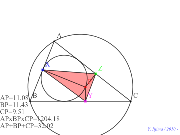
| 00762- シムダン線の前後で何が起こるか？ | 00761- シムダン線の前後で何が起こるか？ | 00760- 基本の図内接円内接円上に点と垂線の足三角形 | 00759- 内接円上に点と垂線の足の距離の和と積駄目 | 00758- 内接円上に点と頂点の距離の和と積駄目 |
 |  |  |  |  |
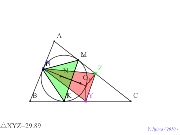
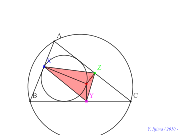
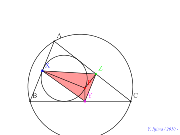
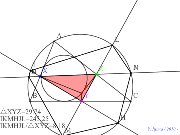
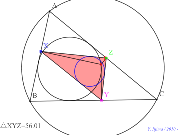
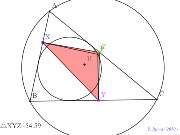
| 00757- 内接円上に点。二つの内心のめ線分の軌跡 | 00756- 内接円上に点。二つの外心のめ線分の軌跡 | 00755- 内接円上に点。二つの重心め線分の軌跡 | 00754- 内接円上で垂線三角形の一辺の軌跡 | 00753- シムダン線、内接円上に点を乗せる？ |
 |  |  |  |  |
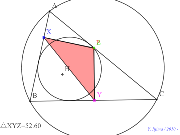
| 00752- シムダン線、内接円上。垂線三角形とできる六角形の面積比駄目 | 00751- シムダン線の軌跡、点を外接円上を動かす | 00750- 内接円上の点からの垂線の足三角形の内接円の軌跡 | 00749- 内接円上の点からの垂線の足三角形の外接円の軌跡 | 00748- 内接円上の点からの垂線の足三角形の内心の軌跡 |
 |  |  |  |  |
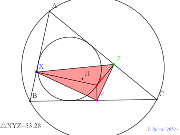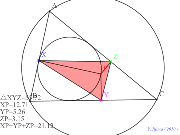
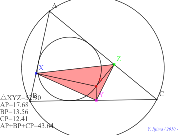
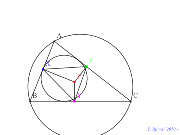
| 00747- 内接円上の点からの垂線の足三角形の外心の軌跡 | 00746- 内接円上の点からの垂心三角形の重心の軌跡 | 00745- 内接円上の点からの距離の和？？ | 00744- 内接円上の点と各頂点の距離の和？？ | 00743- シムダン線、内接円上に点を乗せる？ |
 |  |  |  |  |
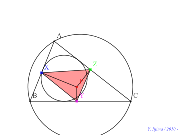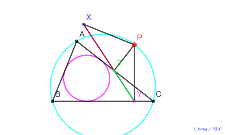
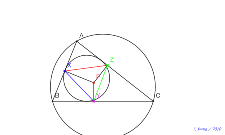
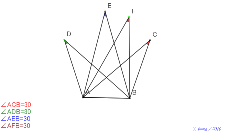
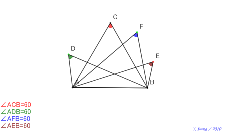
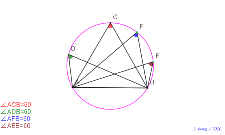
| 00742- シムダン線、外接円上に点を乗せる内接円をかく | 00741- シムダン線、外接円と内接円をかく | 00740- シムダン線、外接円と内接円をかく | 00739- ９月１４日（火曜）高等部２年生３０度の円周角をたくさん | 00738- ９月１４日（火曜）高等部２年生３０度の円周角 |
 |  |  |  |  |
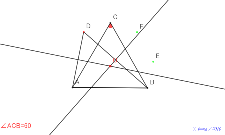
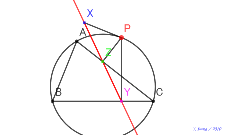
| 00737- ９月１４日（火曜）高等部２年生６０度の円を見る | 00736- ９月１４日（火曜）高等部２年生６０度の円の中心を求める | 00735- ９月１４日（火曜）高等部２年生６０度の円周角 | 00734- 垂線の足三角形と外接円上に乗せる | 00733-垂線の足三角形と外接・内接 |
 |  |  |  |  |
| 00732- シムダン線を見る（外接円上の点P） | 00731- 6個内接円の中心三角形関係は？ | 00730- 6個内接円の中心三角形関係は？ | 00729- 垂線の足からできる6個内接円の中心関係は？ | 00728- 垂線の足からできる6個内接円の中心関係は？ |
 |  |  |  |  |
| 00727- ko_垂線の足からできる6内接円の関係は？ | 00726- 垂線の足からできる内接円の関係は？ | 00725- 垂線の足で分割される辺の線分の比は一定か？ | 00724- 垂線の足結ぶ線分が一直線になるには？ | 00723- 垂線の足の中点三個の三角形の面積は？ |
 |  |  |  |  |
| 00722- 垂線の足の中点三個の軌跡は？ | 00721- 3つの垂線の足、3つの円の一致は？ | 00720- 3つの垂線の足、3つの円の一致は？ | 00719- 3つの垂線の足、3つの円の一致は？ | 00718- 垂線の足三角形の面積最大は？ |
 |  |  |  |  |
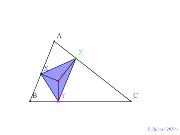| 00717-シムダン線になるまで | 00716- シムダン線になるまで。その2外接円 | 00715- シムダン線になるまで。その1 | 00714- シムダン線になるまで。その1 | 00713- シムダン線になるまで。その1 |
 |  |  |  |  |
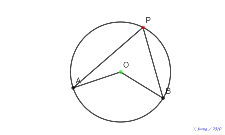| 00712-シムダン線になるまで | 00711-シムダン線になるまで | 00710-シムダン線になるまで | 00709-シムダン線になるまで | 00708- 2021年高等部２年Bチーム円周角と中心角 |
 |  |  |  |  |
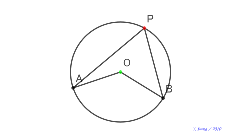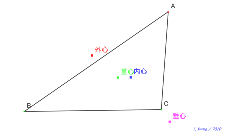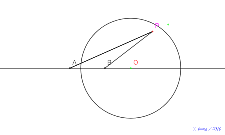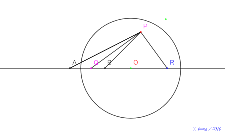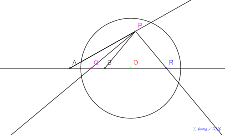
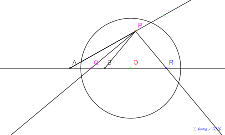
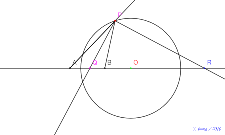
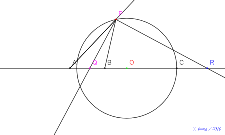
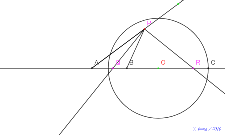
| 00707-nenn2021 | 00706-８月３１日四点を漢字で | 00705-四点を漢字で | 00704- 基本の図８月１３日１６：５８点Pを自由な点に、半直線は書かな い直角三角形の２点の軌跡をとる。アポロニウスの円にする。 | 00703- ８月１３日１６：５８点Pを自由な点に、半直線は書かない直角三 角形の２点の軌跡をとる。アポロニウスの円にする。 |
 |  |  |  |  |
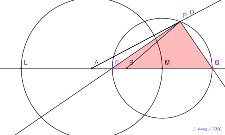
| 00702- ８月１３日１６：５１点Pを自由な点にする。直角三角形の２点の 軌跡をとる。アポロニウスの円にする。 | 00701- ８月１３日１６：５１直角三角形の２点の軌跡をとる。アポロニウ スの円にする。 | 00700- ８月１３日１６：５０直角三角形の２点の軌跡をとる。アポロニウ スの円にする。 | 00699- ８月１３日１６：５０直角三角形の２点の軌跡をとる。ロニウスの 円にする。 | 00698- ８月１３日１１：５０直角三角形の２点の軌跡をとる。ロニウスの 円にする。 |
 |  |  |  |  |
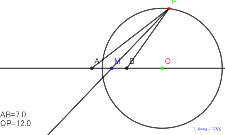
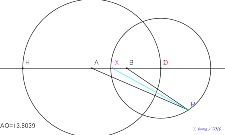
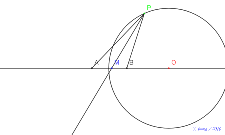
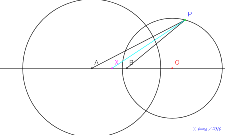
| 00697- ８月１３日１１：４４１４．０９４８１でアポロニウスの円になる 。 | 00696- ８月１３日１１：４０直角三角形色つきアポロニウスの円にする。 | 00695- ８月１３日１１：３７アポロニウスの円にする。 | 00694-半径１２_の円で考える | 00693- ８月10日７_と１２_中心をどこにとればアポロニウスの円と呼 んでよいのか？ |
 |  |  |  |  |
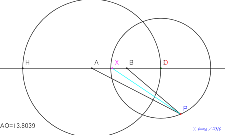
| 00692- ８月10７日中心をどこにとればアポロニウスの円と呼んでよいの か？ | 00691- __８月７日中心をどこにとればアポロニウスの円と呼んでよいの か？ | 00690-これで出来たかな！！ | 00689-13 | 00688-13 |
 |  |  |  |  |
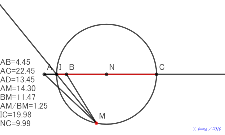
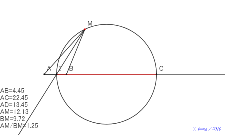
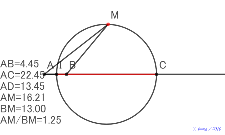
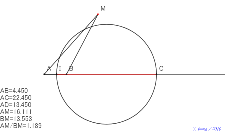
| 00687-13 | 00686- ８月７日中心をどこにとればアポロニウスの円と呼んでよいのか？ | 00685- ８月７日アポロニウスの円するためには？ | 00684- ８月７日アポロニウスの円にならない | 00683- 垂線の足も円の中心も夕方に８月６日のアポロニウスの円比を見つ ける |
 |  |  |  |  |
| 00682- 円の中心も夕方に８月６日のアポロニウスの円比を見つける | 00681- 夕方に８月６日のアポロニウスの円比を見つける | 00680- ８月６日のアポロニウスの円比を見つける | 00679- ８月６日のアポロニウスの円比を見つける | 00678- ８月６日のアポロニウスの円比を見つける |
 |  |  |  |  |
| 00677- ８月６日のアポロニウスの円比を見つける | 00676- アポロニウスの円比を見つける | 00675-アポロニウスの円5_4 | 00674-アポロニウスの円3_1 | 00673-アポロニウスの円 |