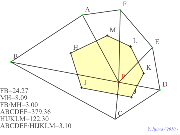[2172-][2072-][1972-][1872-][1772-][1672-][1572-][1472-][1372-][1272-][1172-][1072-][972-][872-][772-][672-][572-]472-, [372-][272-][172-][72-] / sort : [↓-]. ↑
 |  |  |  |  |
| 00472-三角形と三個の重心 | 00471-四角形と四個の重心 | 00470-五角形と五個の重心 | 00469-六角形と6個の重心 | 00468-六角形と6個の重心 |
 |  |  |  |  |
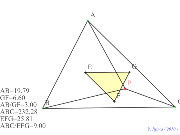
| 00467-四角形と四個の重心 | 00466-五角形と五個の重心 | 00465-四角形と四個の重心 | 00464-三角形と三個の重心 | 00463- 出来た証明その４（対辺平行六角形） |
 |  |  |  |  |
| 00462- 出来た証明その２点Pを直線上に束縛した | 00461-出来た証明その１ | 00460- 出来た１８０度証明を考えるPQ平行Aを通る直線上 | 00459- 証明を考えるPQ平行Aを通る直線上 | 00458-証明を考える |
 |  |  |  |  |
| 00457-三角形分割その２ | 00456-三角形分割その１ | 00455-課題にならない６重心重心 | 00454-問題の図 | 00453-点Pの位置を何処に？ |
 |  |  |  |  |
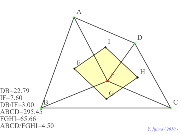
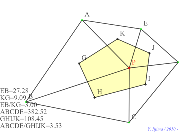
| 00452- 四角形内部二点、六個の重心からの六角形の性質 | 00451- 四角形の内部に二点、6個のめ重心からの | 00450- 五角形と五個の重心からの五角形 | 00449-重心四個 | 00448- 四角形の辺と角の関係（最小と最長が隣同士） |
 |  |  |  |  |
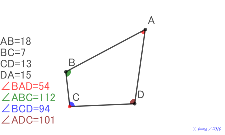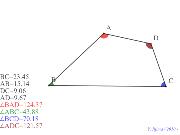
| 00447- 四角形の辺と角の関係（最小と最長が隣同士） | 00446-赤角_緑角。青角_茶色角 | 00445- 新しい4つの辺と4つの角度と対角線の関係？ | 00444- 4つの辺と4つの角度と対角線の関係？ | 00443-4つの辺と4つの角度 |
 |  |  |  |  |
| 00442-4つの辺と4つの角度 | 00441-定番で無い最短距離 | 00440-定番で無い最短距離 | 00439-定番の最短距離 | 00438-定番で無い最短距離 |
 |  |  |  |  |
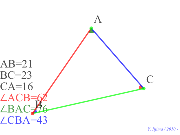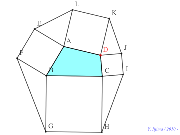
| 00437-定番の最短距離 | 00436-Heronの定理「最短距離 | 00435- 辺と向かい合う角の大小関係は一致 | 00434- 辺と向かい合う角の大小関係は一致 | 00433- 辺と向かい合う角の大小関係は一致 |
 |  |  |  |  |
| 00432- 名古屋の三角形と余弦定理その2 | 00431- 名古屋の三角形と余弦定理その2 | 00430-名古屋の三角形その1 | 00429-点Dだけ動く4個の正方形 | 00428-点Aだけ動く三個の正方形 |
 |  |  |  |  |
| 00427-点Aだけ動く三個の正方形 | 00426-点Aだけ動く | 00425- Xを動かすと角度変化する。最短ルート！お花畑と梨畑！角度一定 | 00424- 最短ルート！お花畑と梨畑！角度一定 | 00423-最短ルート！お花畑 |
 |  |  |  |  |
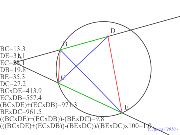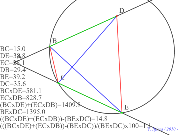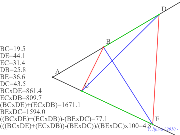| 00422- 三角形分割と4つの重心からの四角形 | 00421- 点Dを右外に出しても差はそれ程大きくならない円を描く対辺の積 の和の二割程度の差トレミー_の定理が何故その32 | 00420- 外接円を描く対辺の積の和の二割程度の差トレミー_の定理が何故 その32 | 00419- 対辺の積の和の二割程度の差トレミー_の定理が何故その32 | 00418- 余り大きく数値が変化しないトレミー_の定理が何故その2 |
 |  |  |  |  |
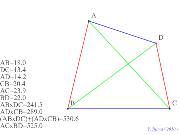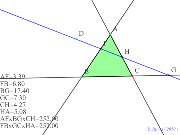
| 00417-トレミーの定理が何故その1 | 00416-円をかくトレミーの定理 | 00415- 円をかくトレミーの定理の準備計算 | 00414-トレミーの定理の準備計算 | 00413- メネラウスの定理で点は外にも出せる |
 |  |  |  |  |
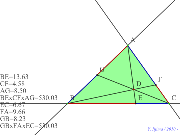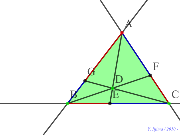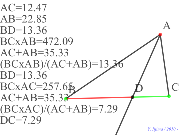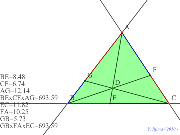
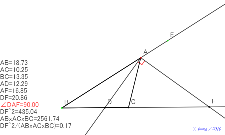
| 00412- チェバの定理で点は外にも出せる | 00411- チェバとメネラウスの定理を一緒にする | 00410- チェバとメネラウスの定理を一緒にする | 00409- 三角形の頂点角二等分線と底辺の線分の長さ | 00408- 三角形の頂点二等分線と底辺の線分の長さの式 |
 |  |  |  |  |
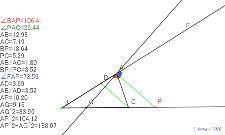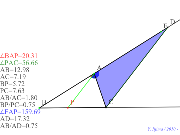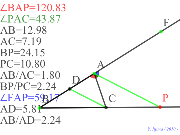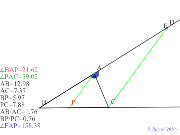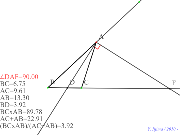
| 00407- これでは三平方？？2月10日近藤実践「角の二等分線と比 | 00406- 三平方と2月10日近藤実践「角の二等分線と比 | 00405- 三角形に色あり2月10日近藤実践「角の二等分線と比 | 00404- 2月10日近藤実践「角の二等分線と比 | 00403- 2月10日近藤実践「角の二等分線と比 |
 |  |  |  |  |
| 00402-3月10日GC課題その7 | 00401-3月10日GC課題その6 | 00400-3月10日GC課題その5 | 00399-3月10日GC課題その4 | 00398-3月10日GC課題その3 |
 |  |  |  |  |
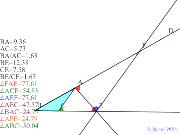
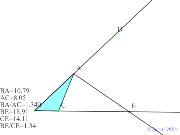
| 00397-3月10日GC課題その2 | 00396-3月10日GC課題その1 | 00395-3月10日GC課題 | 00394- 合同な三角形を確認ニ辺とその間の角の合同条件 | 00393-合同な三角形を確認する！ |
 |  |  |  |  |
| 00392- 2個正方形から合同な三角形をつくろう！ | 00391-近藤実践の課題と結論の証明 | 00390-近藤実践の課題と結論 | 00389-近藤実践その一 | 00388-合同な三角形を作ろう？ |
 |  |  |  |  |
| 00387- 3つの外角の二等分線は、内角の二等分線もかく | 00386-3つの外角の二等分線は？ | 00385-2_10附属の課題 | 00384- 2_10附属の課題の結末は？ | 00383-余弦定理の説明面積の差も |
 |  |  |  |  |
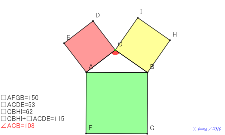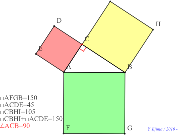
| 00382- 三平方の定理を、点Aを自由な点にした | 00381-余弦定理の説明面積の差も | 00380- 三平方の定理を、点Aを自由な点にした | 00379-三平方の定理を見る | 00378- 辺と対角のcosで割ってみたがだめ。「正弦定理」のsinをc osかえてみたが？ |
 |  |  |  |  |
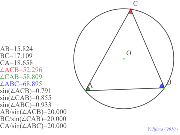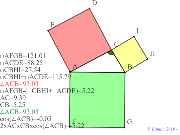
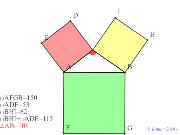
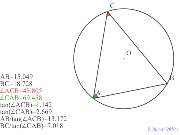
| 00377- 「正弦定理」辺を対角のsinで割ると直径の値になる。 | 00376- 半径無しの比を取る。意味「正弦定理」のsinをcosかえてみ たが？ | 00375- 半径無しの比で。意味「正弦定理」のsinをtanに変えたら？ | 00374- 意味「正弦定理」のsinをtanに変えたら？ | 00373- 意味「正弦定理」のsinをcosかえてみたが？ |