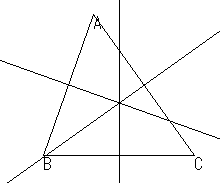
この図では,何が注目に値するのだろう。それは,「3つの直線が1点で交わっている」ということである。しかも,3角形を動かしても,「いつでも1点で交わる」ということである。
上では,「3角形の3つの辺の垂直二等分線を引く」という方法で,一つの共点性(外心)が得られたが,これ(作図方法)を変えることによって,他にどんな共点性(いろいろな心)を作ることができるだろうか。

外心		辺の垂直二等分線
内心		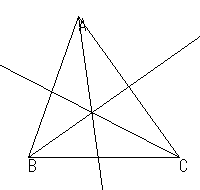角の二等分線
重心		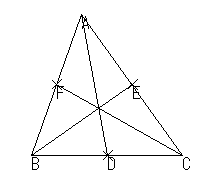中線
垂心		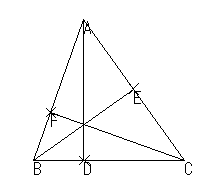頂点から対辺に引いた垂線
傍心		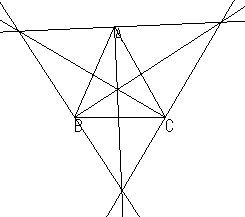外角の2等分線
Fermat点		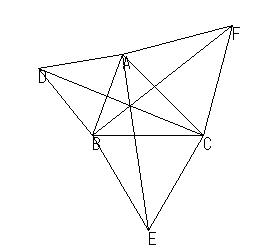3つの辺上に外側に正三角形を作図し,その頂点と対する頂点を結ぶ