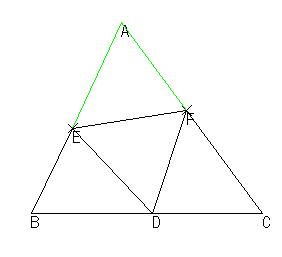
紙でできたΔABCがある。頂点AをBC上に乗せて折る。
点 D の位置を固定しておいて,点 A を移動し,ΔEDB,ΔFBCが相似になる位置を求めたい。

紙でできたΔABCがある。頂点AをBC上に乗せて折る。
点 D の位置を固定しておいて,点 A を移動し,ΔEDB,ΔFBCが相似になる位置を求めたい。
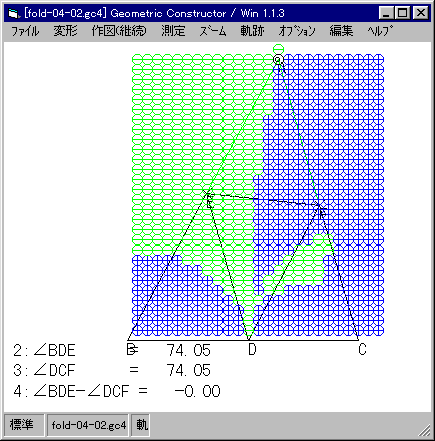
正直言って,予想していたのとはかなり違いました。
(いや,違う部分があったというのが正しいかもしれません。)
大きく分けて,三つの曲線がありますが,それらが生じる原因の一つは,確かに,今調べている「平行性」ですか,一方で,以前,上原さんが指摘された「うまくいかないはず」の場合が大きく影響しています。こういう現象に関しては,「うまくいかないところは最初から排除してしまう」という仕様の方がいいのかもしれません。
なお,「平行性」が成立するのは,上の図のような場合を含め,現在の点 A を含む曲線となります。
しかし,この曲線の様子は分かりにくいので,点 D の位置を変えてみることにしました。
その図が,次の図です。
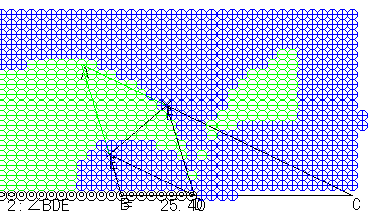
左側をもう少し詳しく見たいので,画面を最大にして,左側について調べました。
その図が次の図です。
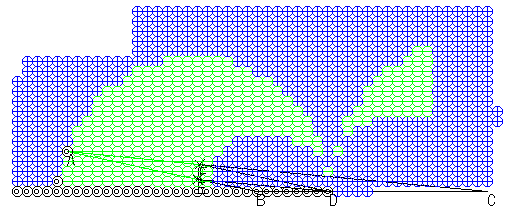
少し色分けをしてみると,次のようになります。
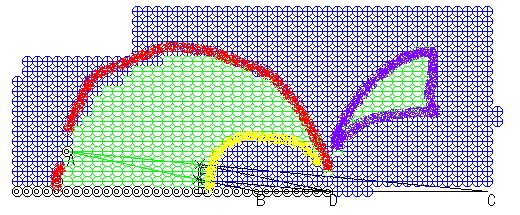
「赤,黄色,紫と三つのブロックがありますが,注目に値するもの,そして適切に扱えそうなものはどれだろうか,」
というのが,これを観察して感じることですね。
(当初から想定していたのは,もちろん,「赤」だけです。)
(黄色や紫に関する探究は,また,後日の課題とするか,あるいはどなたかにお任せすることにしたいと思います。)
そして,一つの想定される流れとしては,
という問いを引き出すということになるでしょう。