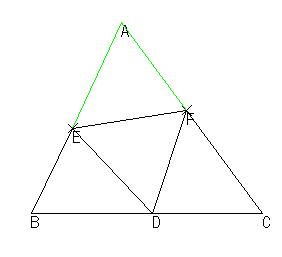
紙でできたΔABCがある。頂点AをBC上に乗せて折る。
点 D の位置を固定しておいて,点 A を移動し,ΔEDB,ΔFBCが相似になる位置を求めたい。

紙でできたΔABCがある。頂点AをBC上に乗せて折る。
点 D の位置を固定しておいて,点 A を移動し,ΔEDB,ΔFBCが相似になる位置を求めたい。
軌跡がどういう円になるかを構成できると, D を変化させたときの変化を観察することは次の自然な流れになるでしょう。
AD,BDを測定します。
Dが AB を AD : BD の比で「内分」しているので,
AB を AD : BD の比で「外分」する点, つまり -AD : BD で内分する点 G を作ります。
そのため,数式で, -AD をその前に作成しておきます。
次に, DE の中点を H とし,
H を中心とし, G を通る円を作成します。
それが,次の図です。
D を動かしたときの円の軌跡を描くと,次のようになります。
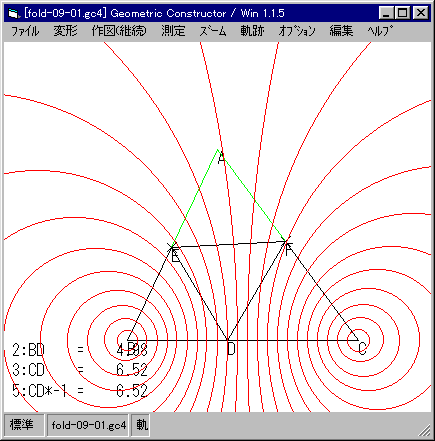
たとえば,次のようなことが分かります。
- D が中点のときには,円ではなく,ABの垂直二等分線(広い意味での円)になる。
- これらの円の族は,交わらない。
- これらの円の族が通過する集合は,A,B 以外のすべての点である。
- しかし,ΔABCが作られる条件を考えると,直線AB以外のすべての点である。
- 点 A をどこにとっても, 二つの三角形が相似になる点が少なくとも一つあることが,このことから分かる。
- ΔABCが正三角形のときにいつでも相似ということは,この図の中には含まれていない。(三角形の相似性の対応の仕方がここで考えているものと違う)