４角→４角
愛知教育大学 数学教室
飯島康之
問題状況
|
|
|
|
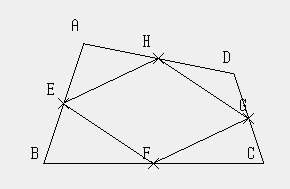
φ:四角形 ABCD → 四角形 EFGH |
|
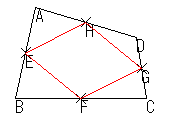
という形をしていることだろう。
つまり,四角形 ABCD を変化させたときに,それを元にできる 四角形 EFGH はどう変わるのかという問題であり, 四角形 EFGH が四角形 ABCD の関数になっているという見方である。
そのため,関連する事例,つまり「四角形→四角形」という事例を集めてみて,
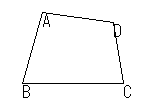
| (元)四角形ＡＢＣＤの４つの辺の中点を結ぶと四角形ＥＦＧＨができる。 |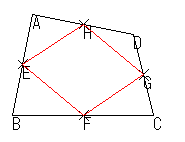 
| 「4角中点」へ |
|
四角形ＡＢＣＤの４つの辺の垂直二等分線のそれぞれの交点を結ぶと四角形ＥＦＧＨができる。 |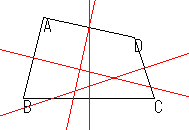 
| 「4角垂2分」へ |
| 四角形ＡＢＣＤの４つの角の二等分線のそれぞれの交点を結ぶと四角形ＥＦＧＨができる。 | 
| 「4角角2分」へ |
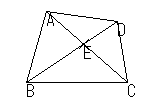4つの3角形 = ΔEAB, ΔEBC, ΔECD, ΔEDA
| それぞれの三角形の内心を結んで三角形を作る |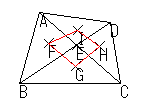 
| |
| それぞれの三角形の外心を結んで三角形を作る |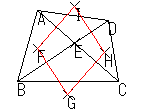 
| |
| それぞれの三角形の重心を結んで三角形を作る |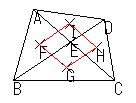 
| |
| それぞれの三角形の垂心を結んで三角形を作る | 
|
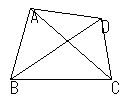4つの3角形 = ΔABC, ΔBCD, ΔCDA, ΔDAB
| それぞれの三角形の内心を結んで三角形を作る |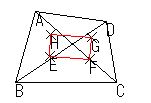 
| |
| それぞれの三角形の外心を結んで三角形を作る |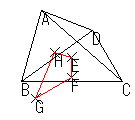 
| |
| それぞれの三角形の重心を結んで三角形を作る |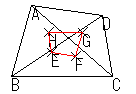 
| |
| それぞれの三角形の垂心を結んで三角形を作る | 
|
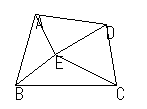4つの3角形 = ΔEAB, ΔEBC, ΔECD, ΔEDA
| それぞれの三角形の内心を結んで三角形を作る |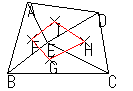 
| |
| それぞれの三角形の外心を結んで三角形を作る |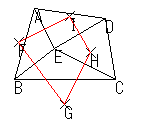 
| |
| それぞれの三角形の重心を結んで三角形を作る |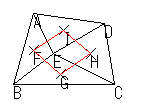 
| |
| それぞれの三角形の垂心を結んで三角形を作る | 
|
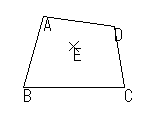
| それぞれの頂点を中心に点対称移動する |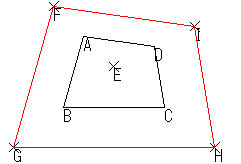 
| |
| それぞれの辺に対して線対称移動する |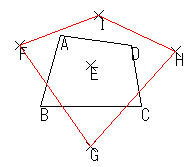 
|
