z ² + z + 1 = 0 の解に関連して

作図の仕方

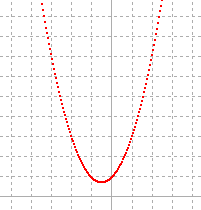
A	独立変数 Z
B	Z2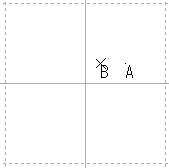
C	Z2 + Z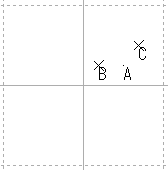
D	定数 1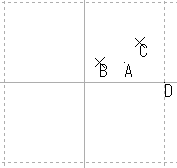
E	Z2 + Z + 1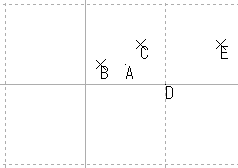

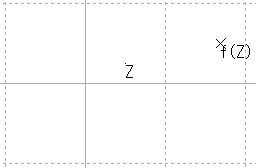
続いて,使いやすくするために,

A 名前を Z にする B 色を消す C 色を消す D 色を消す E 名前を f(Z) にする

実数値関数としての y = x² + x + 1 を複素数化

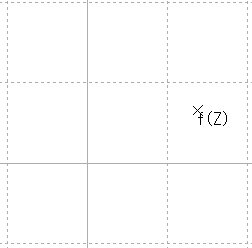
定義域		値域
	→

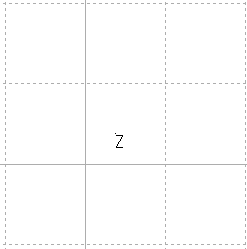これを一つの平面上で重ねたのが,次の図と考えることにする。

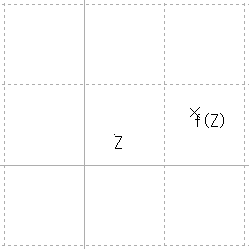
この図の中の独立変数 Z は平面内を動きときに, f(Z) も平面内を動くわけだが,その様子は,次のように軌跡を残すは分かりやすくなる。

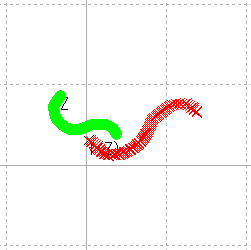
一般に,曲線 γ 上を Z が動けば, γと f(γ)の二つの像が画面内で見ることができる。

「実数解なし」の現象を確認

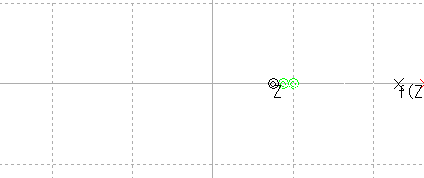	z = 1からスタートして左方向へ。 f(z)が顔を出した。
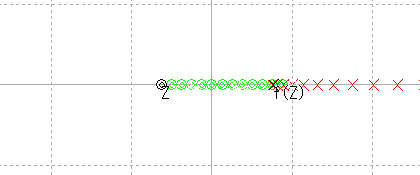	原点が近くなってきたのに, f(z)の動きが鈍くなってきた。
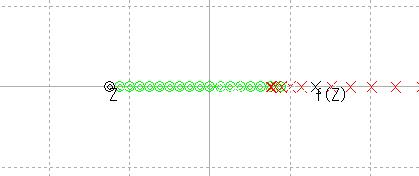	f(z)が右に引き返してしまう。
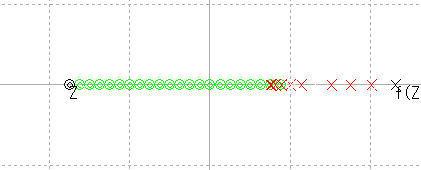	再び f(z)は画面から消え去ろうとしている。

試行錯誤的に解を探す

	z = 1からスタート。
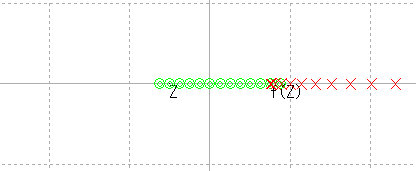	取り敢えず,x軸上をf(z)が最も左に行くあたりまで進んでみる。
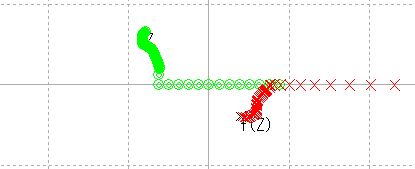	左ではだめだから,少し上の方向にうろうろ。
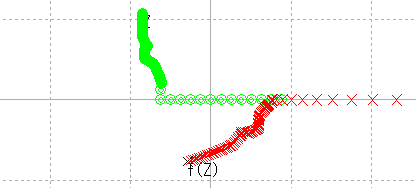	ありゃ,かえって離れてしまう。
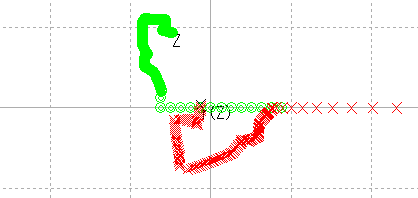	かなりいい線に近づいた感じ。このあたりに解がありそうだ。

組織的に w = f(z) の像について調べる

• 実軸に平行な直線群の像
  

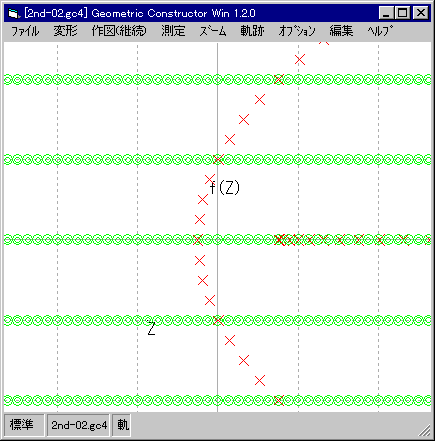  	間隔「1」。
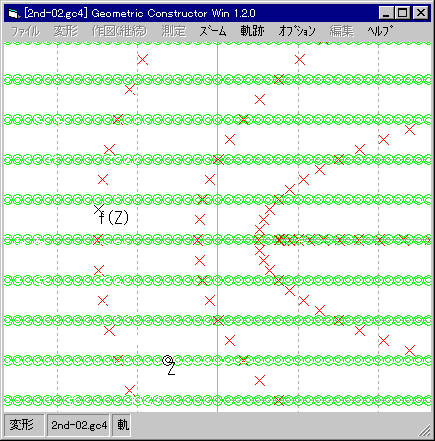  	間隔「0.5」。何本かの放物線。
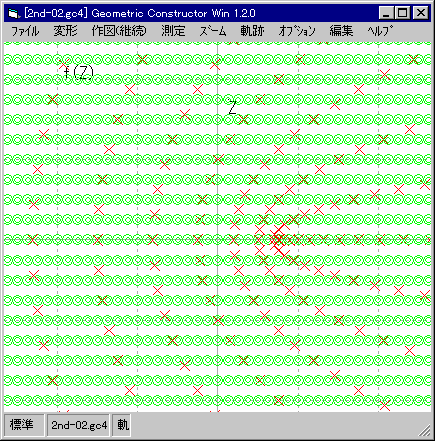  	間隔「0.25」。放物線群が見えてきた。

• 虚軸に平行な直線群の像
  

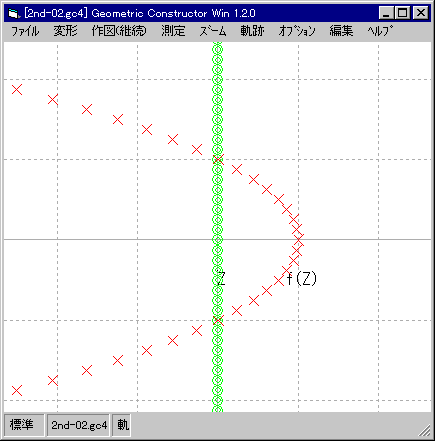  	虚軸の像は,反対向きの放物線。
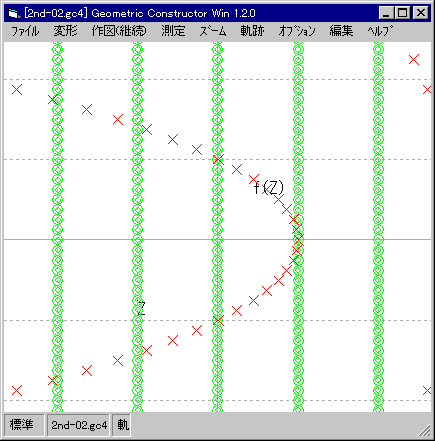  	間隔「1」。
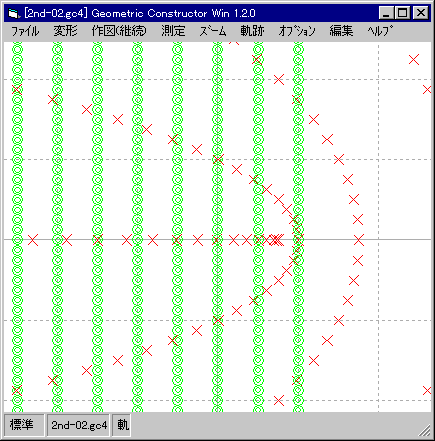  	間隔「0.5」。
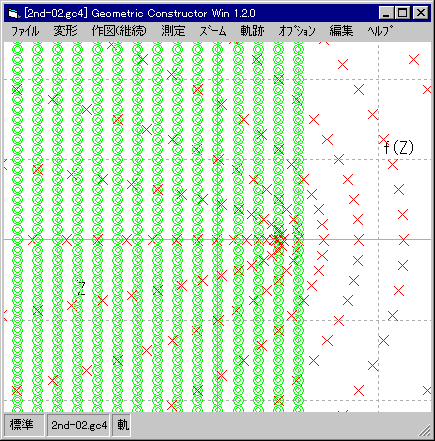  	間隔「0.25」。
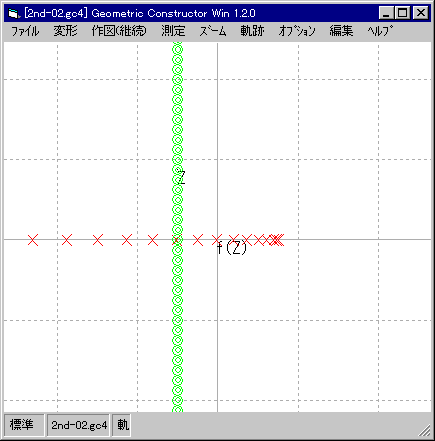  	間隔「0.5」で出てきた半直線に注目。

• 両方を重ねてみると
  

• 単位円の像
  

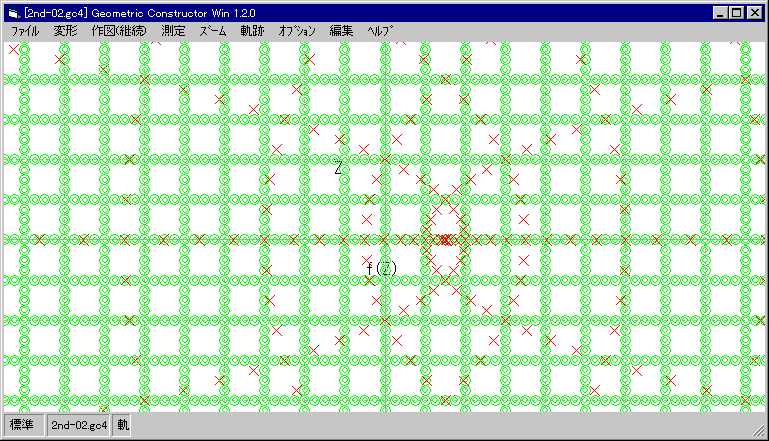
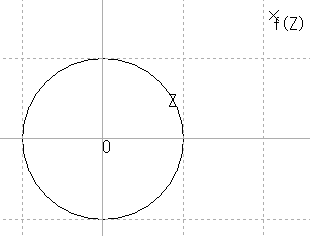  	単位円を追加し,その上に Z の動きを制限する。
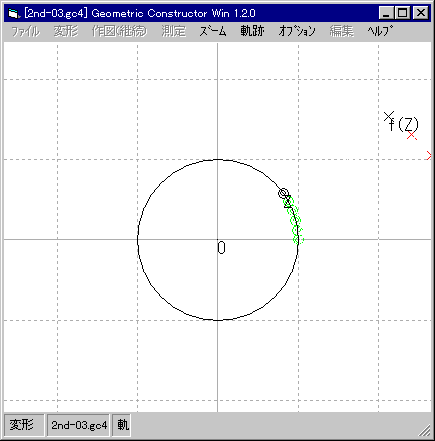  	z = 1 を出発点にして。
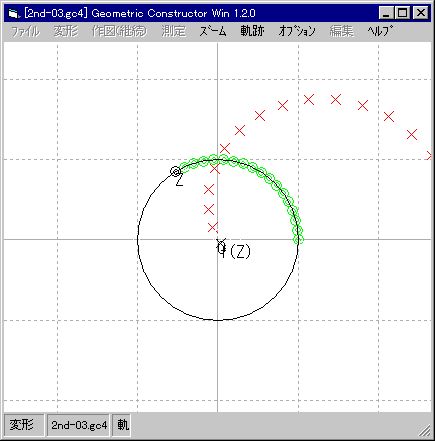  	z = ω で f(z) = 0 になる。
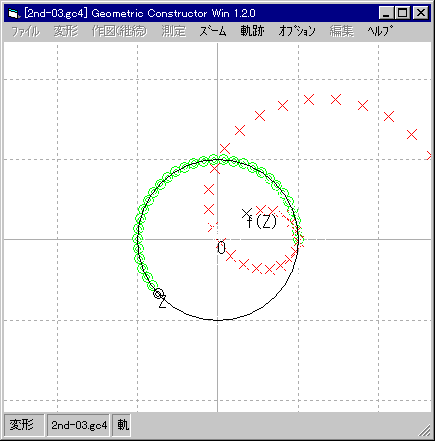  	その後, f(z) の像はクルッと回って
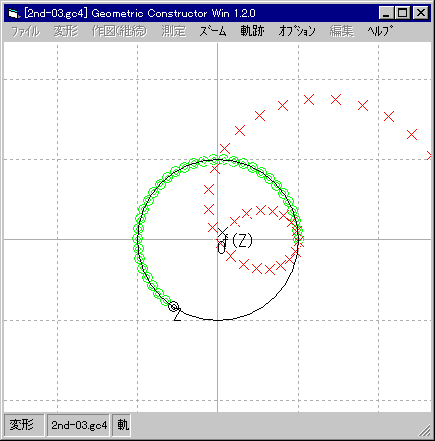  	z = -ωで再び f(z) = 0 になる。
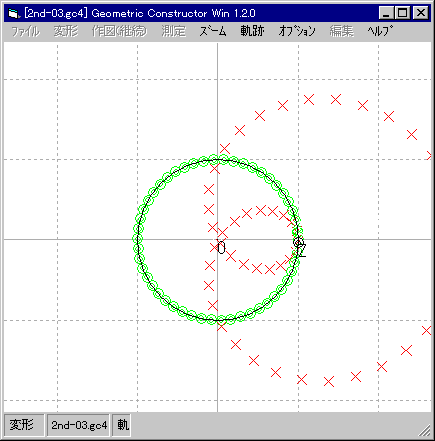  	1周終了。
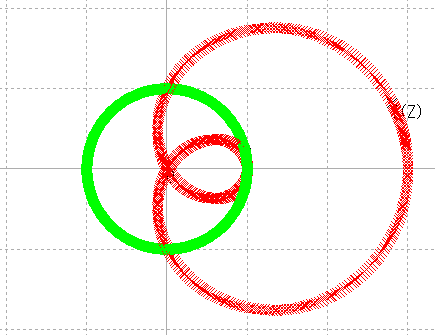  	より細かく軌跡を残して,画面拡大。

• その同心円の像
  

  	r = 0.1
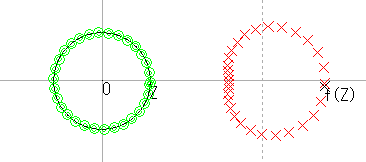  	r = 0.3
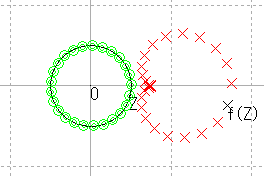  	r = 0.5
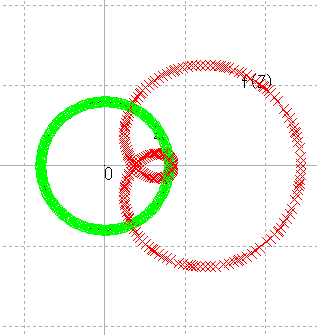  	r = 0.8
  	r = 1
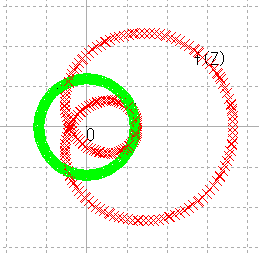  	r = 1.2
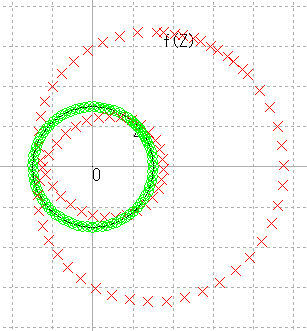  	r = 1.5
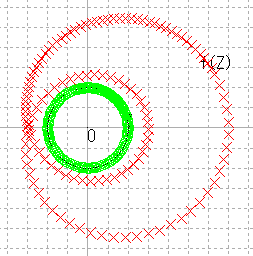  	r = 2

さらに注目してみたいこと

• なぜ放物線が出てくるのか。
• 値が実数になるところ (f^-1(R))が直交するのはなぜか。
• 二つの放物線群は直交しているように見えるが,そうなのか。
• 円の変化の中で,「2重」と「1重」およびその臨界点には何か意味はあるのか。
• 円の中身も考慮すると,r = 1 を境に原点が内部/外部になっているが,それは意味がなるのか。
• 式の係数を変えるとどうなるのか
• 「2」次式でなくなるとどうなるのか