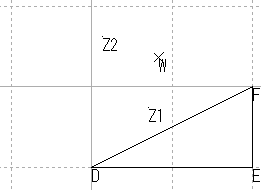
複素数は平面だ。平面上の点に対して,平面上の点を対応させるきまりがあれば,平面内の図形,平面全体などがどのように写るかを調べてみるということは,「写像」としての性質を調べてみることになる。
複素数に関して,様々なものを写像の観点で調べることができるが,まず最初の出発点は四則演算であろう。なお,「差」に関しては「a - b 」は「a + (-b)」と考えられるので,「和」の一部として考えればよい。また「商」に関しては,「a/b」は「a * (1/b)」と考えられることと,GCでは「逆数(1/z)」があるので,「逆数」を考えればよいだろう。そういう意味で,最初の演算は,「和」,「積」,「逆数」とする。
基本的な図形として,次のものを取り上げてみる。
| 対象 | 観点 |
|---|---|
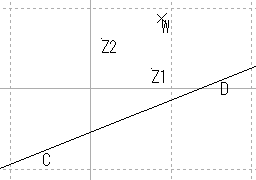
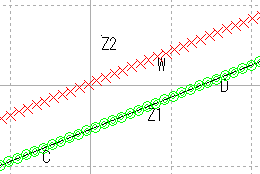
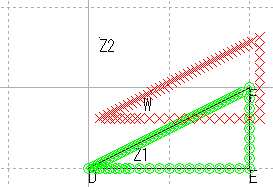
| 直線 | 直線性の保存 |
| 直角三角形 | 直線性/長さ/角度/比 |
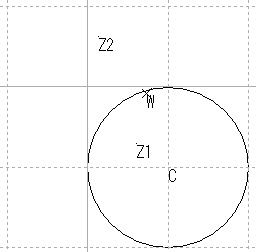
| 円 | 円の保存 |
これまでも「編集」機能の中で,直線や円の上に,点の動きを制限することはできた。しかし,多角形などはその設定を変更しながら行なうとか,キーボードで縦/横のみの動きなどをするしか手がなかった。
GC/Win 1.3.0 以降では,シフトを押しながら変形をするときのモードとして3種類のものを用意した。そのデフォルトは,近接の直線/円の上に点の動きを制限するというもので,要するに,三角形の上などに点の動きを制限することができる。
つまり,シフトを押しながら,矢印キーやマウスを押すことによって,上記のような対象の変換の様子を観察することができる。
| データ | 結果 | |
|---|---|---|
| 直線 |  | 
|
| 直角三角形 | 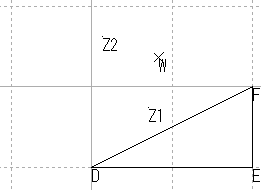 | 
|
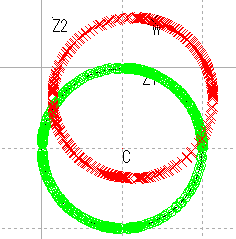
| 円 |  | 
|
| データ | 結果 | |
|---|---|---|
| 直線 | 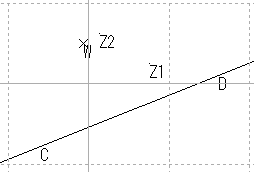 | 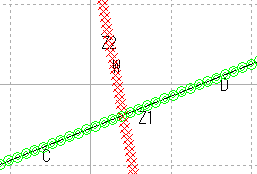
|
| 直角三角形 | 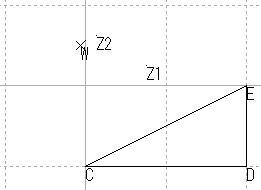 | 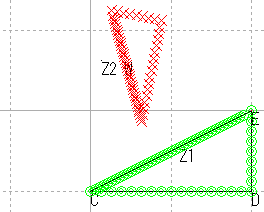
|
| 円 | 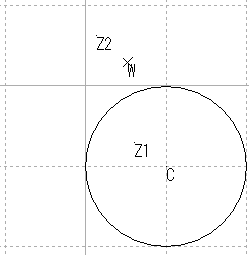 | 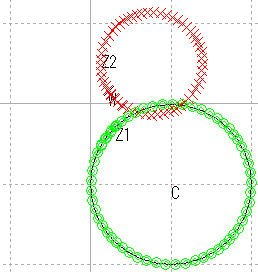
|
| データ | 結果 | |
|---|---|---|
| 直線 | 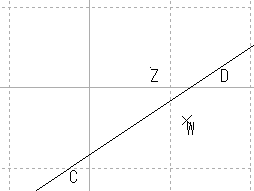 | 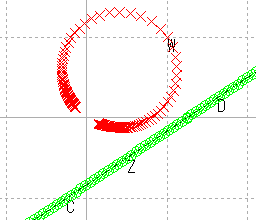
|
| 直角三角形 | 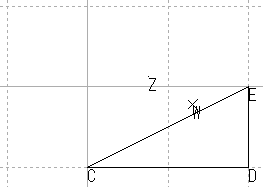 | 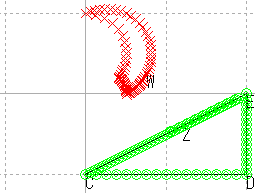
|
| 円 | 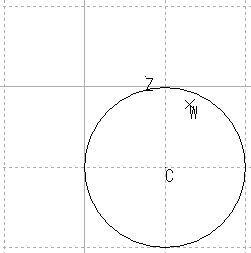 | 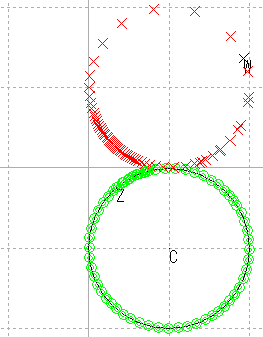
|
上記の結果をまとめると,次のようになる。
| 変換の特徴 | 直線 | 円 | 直角 | 比 | |
|---|---|---|---|---|---|
| 和 | 平行移動 | 直線 | 円 | 直角 | 保たれる |
| 積 | 拡大+回転 | 直線 | 円 | 直角 | 保たれる |
| 逆数 | ? | 円 | 円 | 直角? | 保たれない |