| 変換の特徴 | 直線 | 円 | 直角 | 比 | |
|---|---|---|---|---|---|
| 和 | 平行移動 | 直線 | 円 | 直角 | 保たれる |
| 積 | 拡大+回転 | 直線 | 円 | 直角 | 保たれる |
| 逆数 | ? | 円 | 円 | 直角? | 保たれない |
逆数に関するデータ
| GCデータ | 結果 | |
|---|---|---|
| 直線 | 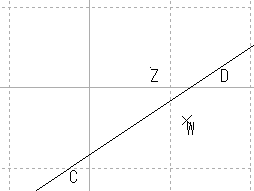 | 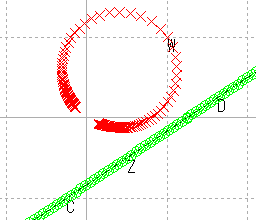
|
| 直角三角形 | 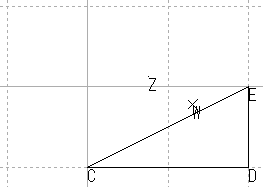 | 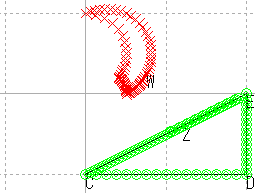
|
| 円 | 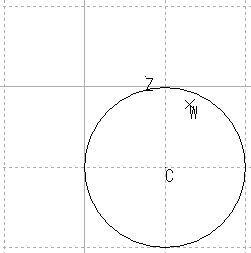 | 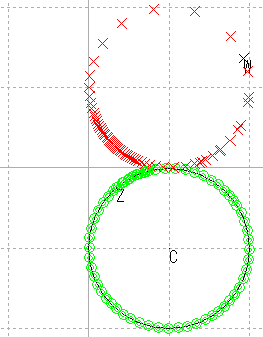
|
| GCデータ | 結果 | |
|---|---|---|
| x軸平行 | 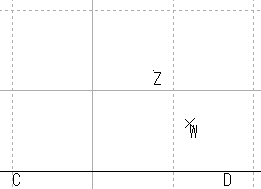 | 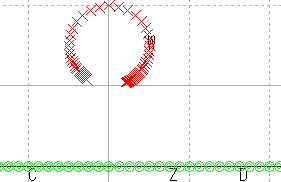
|
| y軸平行 | 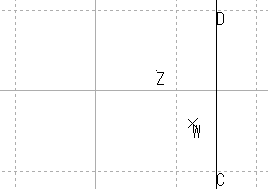 | 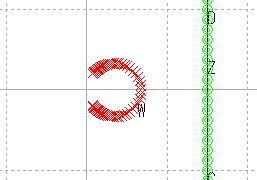
|
| 原点に近い | 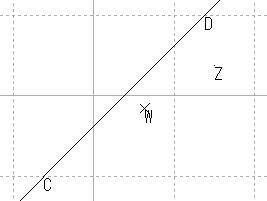 | 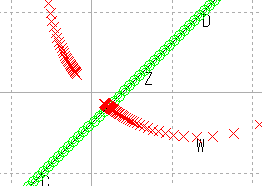
|
| 原点を通る | 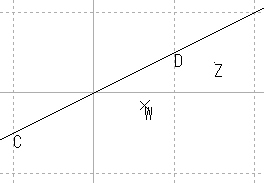 | 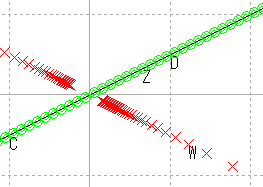
|
これらの結果から,原点を通る直線はやはり原点を通る直線に,原点を通らない直線は,円に写ると推測される。
また,直線を,半径が無限大の円と考えれば,広義の円の集合が広義の円の集合に写ると考えることもできる。
| GCデータ | 結果 | |
|---|---|---|
| 円1 | 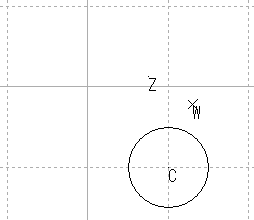 | 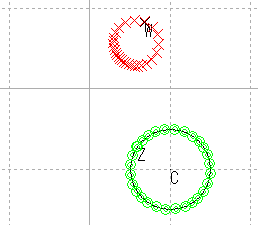
|
| 円2 |  | 
|
| 円3 | 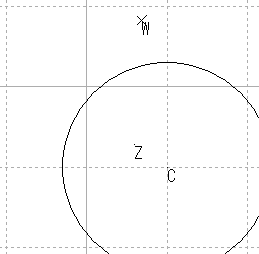 | 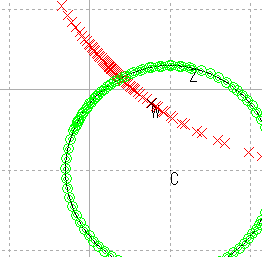
|
| 円4 | 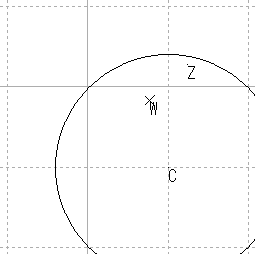 | 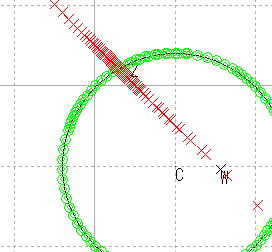
|
| 円5 | 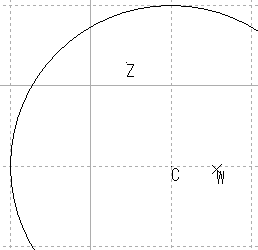 | 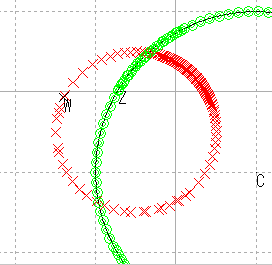
|
以上の結果から,直線の場合の結果をさらに裏付けるべく,
| 変換の特徴 | 直線性 | 広義の円 | |
|---|---|---|---|
| 和 | 平行移動 | 保たれる | 保たれる |
| 積 | 拡大+回転 | 保たれる | 保たれる |
| 逆数 | ? | 保たれない | 保たれる |
角度をどう考えるかはそう簡単ではない。まず,直角の場合を検証してみると,
| まず半直線で角を作る | 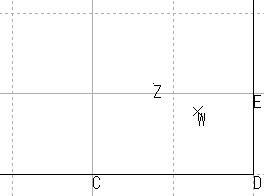
|
| 角の像を描く | 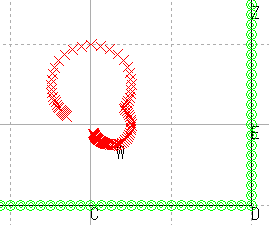
|
| 拡大してみる | 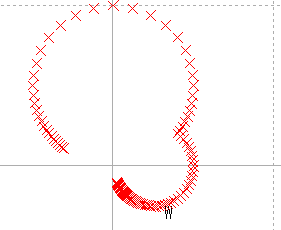
|
| 像に重なる円を追加 | 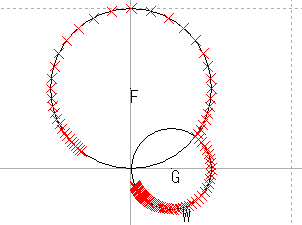
|
| 接線を追加 | 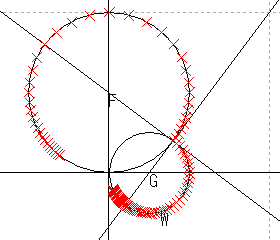
|
このことをいろいろな場合について検証してみれば,直角以外の角に関しても保存されるのかどうかを実験してみることはできよう。
通常の角についても考えるためには,上記では,像に重なると思える円を適当に追加したが,元の角を動かしたときに,この円も動くように,きちんと作図すれば,より確証を得ることができる。円は3点が決まれば決定するので,半直線上にもう一点取り,その像を使って像の円を構成してみることにする。
| まず半直線で角を作る | 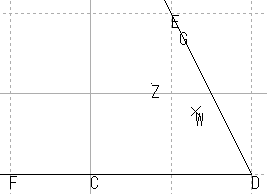
|
| 角の像を描く | 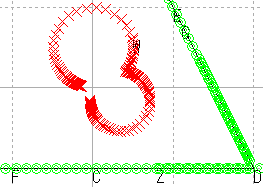
|
| 像の円の候補を作図し測定 | 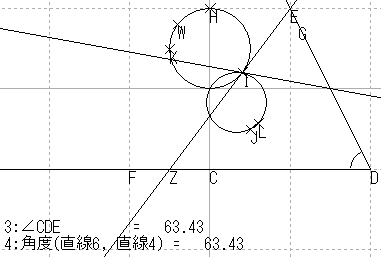
|
| 確認 | 
|
なお,上記では,半直線による角の像を考えたが,より一般に,円と円の角度が保存されることも同様にして確認できる。
以上のことから,少なくとも,逆数の変換は次の特徴を持つことがわかった。
上記の特徴に関しては,これまでの,「和」,「積」に関しても成立する。そのため,次のような演算に関しても,上記の特徴は成立する。
さらに,次のような式を調べてみる価値はあるだろう。