はじめに/「図形を動かす」ことは,私たちにどんな意味があるのだろう。
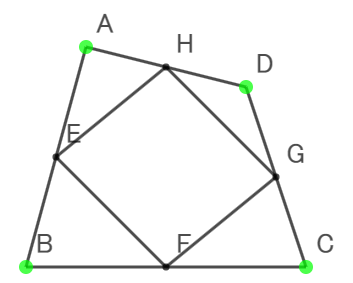
- 紙だから,そこに書き込みをしたり,折ったり,切ったりすることができる。
- 紙の中に書かれている図は,「そういう操作」をしながら,数学的探究を深めていく上で,とても豊富な世界だ。
- この図は(クリックしてGCの環境で開けば)動かすことができる。
- マウス,タッチ,キーボードなどで,一つあるいは複数の頂点を動かしながら観察できる。
- 書き込みはできるけど,折ったり切ったりすることはできない。
- でも,作図の追加をしたり,測定をしたり,軌跡を残したりすることなど,この環境だからできることもある。
- 「紙の世界」と「GCの世界」あるいは「動的幾何の世界」は,にているようで,かなり違うところもある。
深くつきあってみないと,なかなかわからない。
- でも,長くつきあってみないと,深くつきあってみないとわからないことも多い。
教科書などの世界は,「紙で最適化」されているから,「動的なら当たり前」がわかりにくいこともある
- 学校教育で扱う図形は,紙だけではなく,いろいろな教具も使ったりする。
- でも,基本的には,紙で扱える世界の中に最適化されている。
- そこで扱いにくいものは,最初から「ない」のが普通だ。
- 紙の流儀に合わせて「動的」を使おうとすると,不自然なこともある。
- 「動的」での自然なことは,紙の世界では扱われていないこともある。
広がりも,....
- 「同じようなこと」は,他のいろいろな場合にも通用する。
- 紙の場合,ちょっと複雑になると,現実的でないから,「実質的にその図だけに使う」こともある。
- そうなると,「数学的にちゃんとわかったら,もう卒業しよう」というのが,算数・数学での基本的なスタンスだ。
- でも,ICT活用の世界では,「それを使いこなす」ことが大切だったりする。
- 紙の世界では「ここまで」になっていた,その向こう側の世界まで見渡すことがGCや動的幾何の世界では大切だ。
たぶん,そういうことは,「ICTを使いこなすため」には必要
- 数学でのICT活用のケーススタディにもなるでしょう。
- より広く,教育の中で,「探究の道具としてICTを位置づける」ときのケーススタディにもなるでしょう。
この「探究」という世界では,それらを深めたい
- (2) 抽象的に考える → 「プロセス」の定式化など