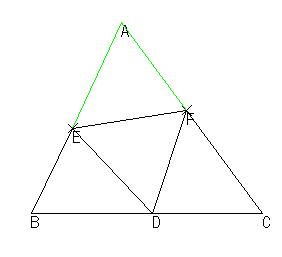
紙でできたΔABCがある。頂点AをBC上に乗せて折る。
点 D の位置を固定しておいて,点 A を移動し,ΔEDB,ΔFBCが相似になる位置を求めたい。

紙でできたΔABCがある。頂点AをBC上に乗せて折る。
点 D の位置を固定しておいて,点 A を移動し,ΔEDB,ΔFBCが相似になる位置を求めたい。
結果が円になりそうだということを観察して,「それはなぜか」と考える場合にしろ,結果を観察せずに,角の二等分線が通るという条件から推論する場合にしろ,それがアプロニウスの円に結びつくということが分かれば,「証明」にたどり着くことになります。
観察のみからアプローチする場合には,「なぜかは分からないが,こういう円になる」ということが経験的にのみ分かるという場合もありえるかもしれません。
逆に,作図ツールで調べるという方法が使えない場合には,このアプローチに到達できる場合は,紙と鉛筆等だけでも解決にいたれる,ということになるでしょう。
定点 A,B がある。PA : PB = m ; n になる点 P の集合は,線分 AB をm : n にそれぞれ内分,外分する点 C,D を直径とする円になる。
PA : PB = 1 : 2 の場合の元になる図
軌跡を求めた結果
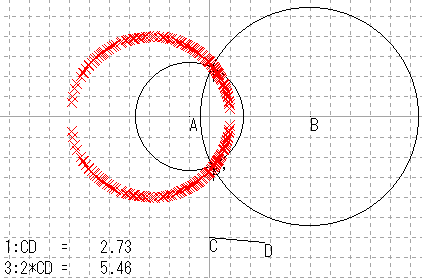
1 : 2 に内分/外分する点とそれを直径とする円の追加