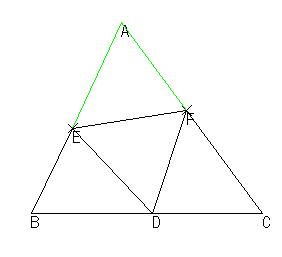
紙でできたΔABCがある。頂点AをBC上に乗せて折る。
点 D の位置を固定しておいて,点 A を移動し,ΔEDB,ΔFBCが相似になる位置を求めたい。

紙でできたΔABCがある。頂点AをBC上に乗せて折る。
点 D の位置を固定しておいて,点 A を移動し,ΔEDB,ΔFBCが相似になる位置を求めたい。
ラフに調べると,ラフな結果しか得られません。
もう少し精密に描ける方法を考えるというのが,一つのアプローチと言えます。
つまり,手作業で 「Dを通るようにする」のではなく,常に角の二等分線が D を通るようにするには,どうしたらいいかということです。
頂角の二等分線との交点が D となっている場合に,どういう関係が成立しているのかを,考えてみます。すると,次のような関係があります。
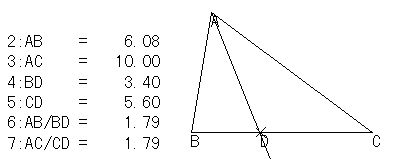
AB : BD = AC : CD
これを,うまく生かす手はないでしょうか。
上の式は,たとえば,
AB : AC = BD : CD
と読めますが,
AB = k BD , AC = k CD
とおけます。
BD,CDを測定しておいて,変数としての k を変化させる / あるいは,変化させてその長さを使うための EF を用意して,それを使うというようなことをすれば,長さとしての AB, AC が決まるので,二つの円を作図し,その交点として A を作ることができます。
具体的な図を,次にあげます。
この中の不必要なところの色を消し,この問題に必要なものを追加します。
条件を満たす点の集合は,ほぼまちがいなくBC上に直径を持つ円(上部のみを考えるならば半円)になるということ